在中國古代著名數學著作《孫子算經》卷下第28题,叫做“物不知數”,原文如下:
有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二。问物几何?
即,一個整數除以三餘二,除以五餘三,除以七餘二,求這個整數。
克罗内克符号
使用该符号,即可给出上述一般同餘方程组的求解过程,分两步完成
#include<stdio.h>
#define DBG 1
int w[3],b[3];
int extgcd(int a, int b, int & x, int & y){
if (b == 0) { x=1; y=0; return a; }
int d = extgcd(b, a % b, x, y);
int t = x; x = y; y = t - a / b * y;
return d;
}
int china(int k){
int i, d, x, y, m, a = 0, n = 1;
for (i = 0; i < k; i++) n *= w[i];
for (i = 0; i < k; i++) {
m = n / w[i];
d = extgcd(w[i], m, x, y);
a += (y * m * b[i]) % n;
if(DBG)printf("a y m b %d %d %d %d\n",a,y,m,b[i]);
}
if (a > 0) return a;
else return (a + n);
}
int main(){
w[0]=3,w[1]=5,w[2]=7,b[0]=0,b[1]=3,b[2]=4;
int ans = china(2);
printf("ans: %d\n",ans);
}
 用一个常用
用一个常用 表示,称之为
表示,称之为
 ,先求出
,先求出 满足
满足 ,即所求的
,即所求的 ,但被每个
,但被每个 整除。其求法如下:记
整除。其求法如下:记 ,根据条件
,根据条件 两两互素,可知
两两互素,可知 和
和 也互素,故存在整数
也互素,故存在整数 和
和 使得
使得 .令
.令 ,则对每个
,则对每个 ,相对应的
,相对应的 显然
显然 ,则
,则 ,这说明
,这说明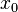 为上述同餘方程组的一个解,从而所有的解可表示为
为上述同餘方程组的一个解,从而所有的解可表示为 ,其中的n可以取遍所有的整数。
,其中的n可以取遍所有的整数。
沒有留言:
張貼留言