The Problem
Football the most popular sport in the world (americans insist to call it "Soccer", but we will call it "Football"). As everyone knows, Brasil is the country that have most World Cup titles (four of them: 1958, 1962, 1970 and 1994). As our national tournament have many teams (and even regional tournaments have many teams also) it's a very hard task to keep track of standings with so many teams and games played!
So, your task is quite simple: write a program that receives the tournament name, team names and games played and outputs the tournament standings so far.
A team wins a game if it scores more goals than its oponent. Obviously, a team loses a game if it scores less goals. When both teams score the same number of goals, we call it a tie. A team earns 3 points for each win, 1 point for each tie and 0 point for each loss.
Teams are ranked according to these rules (in this order):
- Most points earned.
- Most wins.
- Most goal difference (i.e. goals scored - goals against)
- Most goals scored.
- Less games played.
- Lexicographic order.
The Input
The first line of input will be an integer N in a line alone (0 < N < 1000). Then, will follow N tournament descriptions. Each one begins with the tournament name, on a single line. Tournament names can have any letter, digits, spaces etc. Tournament names will have length of at most 100. Then, in the next line, there will be a number T (1 < T <= 30), which stands for the number of teams participating on this tournament. Then will follow T lines, each one containing one team name. Team names may have any character that have ASCII code greater than or equal to 32 (space), except for '#' and '@' characters, which will never appear in team names. No team name will have more than 30 characters.
Following to team names, there will be a non-negative integer G on a single line which stands for the number of games already played on this tournament. G will be no greater than 1000. Then, G lines will follow with the results of games played. They will follow this format:
team_name_1#goals1@goals2#team_name_2
For instance, the following line:
Team A#3@1#Team B
Means that in a game between Team A and Team B, Team A scored 3 goals and Team B scored 1. All goals will be non-negative integers less than 20. You may assume that there will not be inexistent team names (i.e. all team names that appear on game results will have apperead on the team names section) and that no team will play against itself.
The Output
For each tournament, you must output the tournament name in a single line. In the next T lines you must output the standings, according to the rules above. Notice that should the tie-breaker be the lexographic order, it must be done case insenstive. The output format for each line is shown bellow:
[a]) Team_name [b]p, [c]g ([d]-[e]-[f]), [g]gd ([h]-[i])
Where:
- [a] = team rank
- [b] = total points earned
- [c] = games played
- [d] = wins
- [e] = ties
- [f] = losses
- [g] = goal difference
- [h] = goals scored
- [i] = goals against
There must be a single blank space between fields and a single blank line between output sets. See the sample output for examples.
Sample Input
2
World Cup 1998 - Group A
4
Brazil
Norway
Morocco
Scotland
6
Brazil#2@1#Scotland
Norway#2@2#Morocco
Scotland#1@1#Norway
Brazil#3@0#Morocco
Morocco#3@0#Scotland
Brazil#1@2#Norway
Some strange tournament
5
Team A
Team B
Team C
Team D
Team E
5
Team A#1@1#Team B
Team A#2@2#Team C
Team A#0@0#Team D
Team E#2@1#Team C
Team E#1@2#Team D
Sample Output
World Cup 1998 - Group A
1) Brazil 6p, 3g (2-0-1), 3gd (6-3)
2) Norway 5p, 3g (1-2-0), 1gd (5-4)
3) Morocco 4p, 3g (1-1-1), 0gd (5-5)
4) Scotland 1p, 3g (0-1-2), -4gd (2-6)
Some strange tournament
1) Team D 4p, 2g (1-1-0), 1gd (2-1)
2) Team E 3p, 2g (1-0-1), 0gd (3-3)
3) Team A 3p, 3g (0-3-0), 0gd (3-3)
4) Team B 1p, 1g (0-1-0), 0gd (1-1)
5) Team C 1p, 2g (0-1-1), -1gd (3-4)
© 2001 Universidade do Brasil (UFRJ). Internal Contest 2001.
sorting, notice 'case insensitive'
useful scanf method:
scanf ("%[^#]#%d@%d#%[^\n]\n", team1, &goalsForTeam1, &goalsForTeam2, team2);
#include<stdio.h>
#include<string.h>
#include<iostream>
#include<vector>
#include<map>
#include<algorithm>
#define REP(i, b, n) for (int i = b; i < n; i++)
#define rep(i, n) REP(i, 0, n)
#define DBG 0
using namespace std;
string lower(string s){
rep(i,s.size())s[i]=tolower(s[i]);
return s;
}
struct Team{
Team(string a):name(a){name2=lower(name),win=lose=pts=tie=games=gd=gd1=gd2=0;}
string name,name2;
int win,lose,tie, pts,games, gd, gd1,gd2;
};
map<string,int>mp;
vector<Team>tv;
bool comp(Team a,Team b){
if(a.pts!=b.pts)return a.pts>b.pts;
if(a.win!=b.win)return a.win>b.win;
if(a.gd!=b.gd)return a.gd>b.gd;
if(a.gd1!=b.gd1)return a.gd1>b.gd1;
if(a.games!=b.games)return a.games<b.games;
return a.name2<b.name2;
}
void ans(){
sort(tv.begin(),tv.end(),comp);
rep(i,tv.size())
printf("%d) %s %dp, %dg (%d-%d-%d), %dgd (%d-%d)\n",i+1,tv[i].name.c_str(),tv[i].pts,
tv[i].games,tv[i].win,tv[i].tie,tv[i].lose,tv[i].gd,tv[i].gd1,tv[i].gd2);
}
int main(){
int a,b,c,i1,i2,r1,r2,tmp;
char nds[105];
string ts;
bool ll=0;
scanf("%d ",&a);
rep(i,a){
tv.clear(),mp.clear(),c=0;
scanf("%[^\n]\n",nds);
ts=nds;
scanf("%d ",&b);
rep(i,b){
scanf("%[^\n]\n",nds);
mp[nds]=c++;
tv.push_back(Team(nds));
if(DBG)printf("team %s\n",nds);
}
scanf("%d ",&b);
rep(i,b){
char t1[35],t2[35];
int n1,n2;
scanf("%[^#]#%d@%d#%[^\n]\n", t1, &n1, &n2, t2);
if(DBG){printf("%s %d:%d %s\n",t1,n1,n2,t2);}
r1=mp[t1],r2=mp[t2];
if(n1!=n2){
if(n1<n2){tmp=r1,r1=r2,r2=tmp,tmp=n1,n1=n2,n2=tmp;}
tv[r1].win++,tv[r1].gd+=n1-n2,tv[r1].gd1+=n1,tv[r1].gd2+=n2,tv[r1].pts+=3;
tv[r2].lose++,tv[r2].gd+=n2-n1,tv[r2].gd1+=n2,tv[r2].gd2+=n1;
}else{
tv[r1].tie++,tv[r1].gd1+=n1,tv[r1].gd2+=n2,tv[r1].pts+=1;
tv[r2].tie++,tv[r2].gd1+=n2,tv[r2].gd2+=n1,tv[r2].pts+=1;
}
tv[r1].games++,tv[r2].games++;
}
scanf(" ");
if(ll)printf("\n");ll=1;
printf("%s\n",ts.c_str());
ans();
}
}
 用一个常用
用一个常用 表示,称之为
表示,称之为
 ,先求出
,先求出 满足
满足 ,即所求的
,即所求的 ,但被每个
,但被每个 整除。其求法如下:记
整除。其求法如下:记 ,根据条件
,根据条件 两两互素,可知
两两互素,可知 和
和 也互素,故存在整数
也互素,故存在整数 和
和 使得
使得 .令
.令 ,则对每个
,则对每个 ,相对应的
,相对应的 显然
显然 ,则
,则 ,这说明
,这说明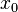 为上述同餘方程组的一个解,从而所有的解可表示为
为上述同餘方程组的一个解,从而所有的解可表示为 ,其中的n可以取遍所有的整数。
,其中的n可以取遍所有的整数。

